planimetria M;): W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C wpisano okrąg. Punkt P jest punktem styczności okręgu z przeciwprostokątną . oblicz długość przyprostokątnych trójkąta , jeśli wiadomo ze |AP|=9 i |PB|=6 Pomorze ktoś ? Bardzo proszę o pomoc

ICSP: (x+9)² + (x+6)² = 15². Znajdz x i dodaj to do odcinków 9 i 6. Wyniki będą przyprostokątnymi.

ICSP: P.S. pomoże przez ż

M;): Właśnie też zauważyłam ten niewybaczalny błąd Sory to z pośpiechu

M;): ale możesz mi wyjaśnić dlaczego (x+9) i (x+6) ? bo rozumiem że jest to działanie na zasadzie Pitagorasa ...

ICSP: Będę rysował wiec to troszkę potrwa.

M;): Okey Dziękuję bardzo !

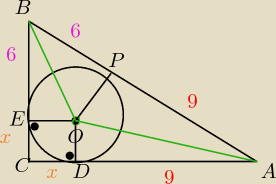
ICSP: Załóżmy że jest wpisany w ten trójkąt. Załóżmy również że O jest środkiem okręgu Styczne są do przyprostokątnych oraz przeciw prostokątnych pod kątem prostym. Czworokąt CDOE jest kwadratem i to chyba widać. odcinek EC = CD = promieniowi okręgu wpisanego = (w moim przykładzie) x) Rozpatrzmy trójkąty ODA i OPA. Mają one jeden wspólny bok(przeciwprostokątną na rysunku oznaczoną zielonym). Mają również inny bok taki sam(promień okręgu wpisanego). Skoro tak jest to z trójkątów przystających wiemy że |DA| = |PA| . Tak samo dla drugiego trójkąta z zieloną. odcinek A = 9 + 6 = 15 Odcinek AC = x + 9 docinek BC = x + 6 Teraz masz twierdzenie pitagorasa.

M;): Dziękuję że tak bardzo przejrzyściej to wyjaśniłeś

ICSP: Spoko. Jakbys miał/a jakieś pytania to wal śmiało.

paula;): Niech ABC będzie tym trójkątem. Ponieważ I AP I = 9 oraz I PB I = 6, zatem I AB I = 9 + 6 = 15 Niech r będzie promieniem okręgu wpisanego w ten trójkąt oraz P i S to punkty styczności okręgu z bokiem BC oraz bokiem AC. O − środek okręgu wpisanego OP = OR = OS = r Łatwo wykazać, ze trójkąt ASO jest przystający do trójkąta APO, zatem I AS I= I AP I = 9 Analogicznie trójkąt BRO jest przystający do trójkąta BPO, zatem I BR i = I BP I = 6 Mamy więc I AC I = r + 9 oraz I BC I = r + 6 Z tw. Pitagorasa mamy I AC I ² + I BC I ² = I AB I ² czyli (r +9)² + (r + 6)² = 15² r² + 18 r + 81 +r² + 12 r + 36 = 225 2 r² + 30 r − 108 = 0 / : 2 r² + 15 r − 54 = 0 delta = 15² − 4*1*(−54) = 225 + 216 = 441 p(delty) = p(441) = 21 r = [ −15 − 21]/2 < 0 <−− odpada r = [ −15 + 21]/2 = 6/2 = 3 ====================== zatem przyprostokątne mają długości: I AC I = 9 + 3 = 12 I BC I = 6 + 3 = 9

Magdalenka: Okrąg o promieniu 1 cm jest wpisany w trójkąt równoramienny o podstawie 4cm. Oblicz długość ramienia trójkąta.

Magdalenka: Niech ktoś pomoże